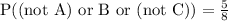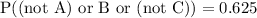Answer:
a)
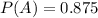
b)
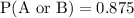
c)
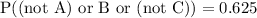
Explanation:
Given : A fair coin is tossed three times and the events A, B, and C are defined as follows: A: At least one head is observed, B: At least two heads are observed, C: The number of heads observed is odd.
To find : The following probabilities by summing the probabilities of the appropriate sample points ?
Solution :
The sample space is
S={HHH,HHT,HTT,HTH,TTT,TTH,THH,THT}
n(S)=8
A: At least one head is observed
i.e. A={HHH,HHT,HTT,HTH,TTH,TTH,THH,THT}
n(A)=7
B: At least two heads are observed
i.e. B={HHH,HTT,TTH,THT}
n(B)=4
C: The number of heads observed is odd.
i.e. C={HHH,HTT,THT,TTH}
n(c)=4
a) Probability of A, P(A)
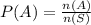
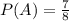
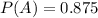
b) P(A or B)
Using formula,

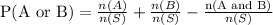
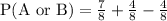

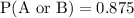
(c) P((not A) or B or (not C))
A={HHH,HHT,HTT,HTH,TTH,TTH,THH,THT}
not A = {TTT} = 1
B={HHH,HTT,TTH,THT}
C={HHH,HTT,THT,TTH}
not C = {HHT,HTH,THH,TTT} = 4
So, not A or B or not C = {HHH,HHT,HTH,THH,TTT}=5