Question

Pedro puts $400.00 into an account to use for school expenses. The account earns 4% interest, compounded annually. How much will be in the account after 5 years? Use the formula A=P1+ r n nt, where A is the balance (final amount), P is the principal (starting amount), r is the interest rate expressed as a decimal, n is the number of times per year that the interest is compounded, and t is the time in years. Round your answer to the nearest cent.

Answer 1

868.76

Explanation:

i did the test

Answer 2

After 5 years the amount in the account will be $ 487.

Explanation:

Compound Interest, A =
`P ( 1 + (r)/(n))^ {nt}`

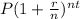
Where A denotes the investment's future value

P is the Principal amount = $ 400.00

r is the rate of interest annually in decimals = 0.04

n is the no. of times the interest is compounded per unit time, t = 1

t - the number of years or days or months the amount is invested = 5 years

Now we have to plug in those values in the above formula as,

A =
`400 ( 1 + (0.04)/(1))^ {1* 5}`

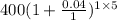
= 400(1+ 0.04)⁵

= 400(1.04)⁵

= 486.66 ≈ $ 487