Answer:
Length of side
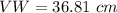 .
.
Explanation:
Diagram of the given scenario is shown below.
Given that:
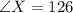 ° ,
° ,
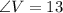 ° and
° and
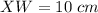
To find : Length of
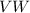 ?
?
So, In
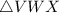
Using Sine law :- Sine law states that the ratio of each side of triangle the sine of the opposite angle is the equal for all three sides and angles. let sides and angle are
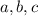 and
and
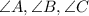 then
then
Sine law :
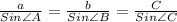
According to Question,
Applying Sine law in
 we get,
we get,
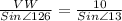
By cross-multiplication
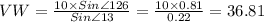
Therefore, Length of side
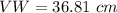 .
.