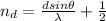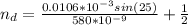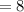Answer:
Part A
There are 7 bright fringes in the angular range
Part B
There are 8 dark fringe in the angular range
Step-by-step explanation:
From the question we are told that the
distance between the slit is
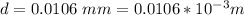
The wavelength is
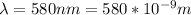
The angle between the center and the brightest fringe =

This destructive interference for bright fringe is mathematically represented as
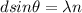
Where n is the number of bright fringe
Making n the subject of the formula
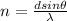
Substituting values
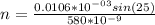
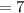
The number of dark fringe is mathematically evaluated as