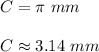Answer:
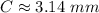
Explanation:
The circumference of a circle can be calculated with the formula shown below:

Where "C" is the circumference of the circle and "r" is the radius.
In this case, according to the information given in the exercise, you know that the radius of the circular base of the object is the following:
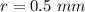
Then, knowing the value of "r", you can substitute it into the formula shown at the beginning of this explanation:
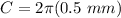
And finally, evaluating and rounding the result to the nearest hundredth, you get that the circumference of the circular base is approximately: