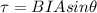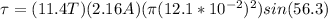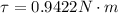Question

A circular wire loop of radius 12.1 cm carries a current of 2.16 A. It is placed so that the normal to its plane makes an angle of 56.3° with a uniform magnetic field of magnitude 11.4 T.

(a) Calculate the magnitude of the magnetic dipole moment of the loop in amperes-square meters.
(b) What is the magnitude of the torque acting on the loop?

Answer 1

To develop this problem we will apply two concepts of electromagnetic physics. The first is the magnetic dipole moment which is defined as the product between the current and the area, and the other is the torque as a function of the magnetic field. Both are described below

The magnetic dipole moment is defined as,

`M = IA`

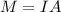
Here,

I = Current

A = Area

At the same time the Torque acting on the loop is given as,

`\tau = BIASin\theta`

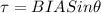
Here,

B = Magnitude of the magnetic field

`\theta` = Angle between magnetic field and the normal to the plane

PART A) The radius of the circular loop is,

`r = 12.1*10^(-2)m`

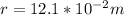
Using the expression of the area in a circle and replacing it in the definition of the magnetic dipole moment we have

`M = IA`

`M = I (\pi r^2)`

`M = (2.16A)(\pi (12.1*10^(-2))^2)`

`M = 0.099A\cdot m^2`

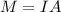
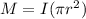
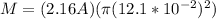
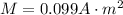
PART B) Using the expression for torque we now have the data of all the variables, therefore replacing them

`\tau = BIA sin\theta`

`\tau = (11.4T)(2.16A)(\pi (12.1*10^(-2))^2)sin(56.3)`

`\tau = 0.9422N\cdot m`