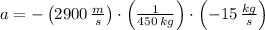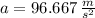Answer:
a)
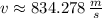 , b)
, b)
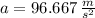
Step-by-step explanation:
a) The maximum speed of the rocket is given by the Tsiolkovski's Equation:
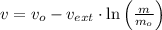
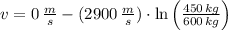
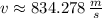
b) The acceleration is obtained by deriving the Tsiolkolski's Equation:
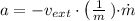
The maximum acceleration occured when fuel is entirely consumed. Then: