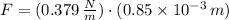Answer:
a)
 , b)
, b)
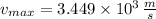 , c)
, c)
 , d)
, d)
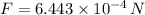 , e)
, e)

Step-by-step explanation:
a) The angular frequency is:
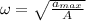

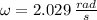
The period of the motion is:
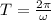
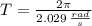

b) The maximum speed of the particle is:
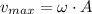
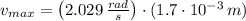
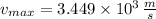
c) The spring constant is:

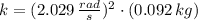

The total mechanical energy of the oscillator is:

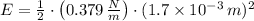

d) The magnitude of the force on the particle at its maximum displacement is:
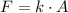
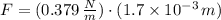
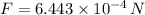
e) The magnitude of the force on the particle at half of its maximum displacement is: