Question

Jenny is arranging 12 cans of food in a row on a shelf. She has 5 cans of beans, 1 can of carrots, and 6 cans of corn. In how many distinct orders can the cans

be arranged if two cans of the same food are considered identical (not distinct)?​

Answer 1

5544 ways

Explanation:

Given that:

Number of cans = 12 (n)

Number of cans of corns = 6 (
`r_(1)`)

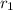Number of cans of carrot = 1
`r_(2)`

Number of cans of beans = 5
`r_(3)`

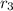
The number of different arrangements is given as:

`(n!)/(r_(1)!* r_(2)!* ...r_(k)!)` where
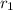`r_(1)` objects are of one kind,
`r_(2)` objects are of another and so on

We have:
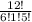`(12!)/(6!1!5!)` = 5544 ways

Hope it will find you well.