Answer:
Option C) 0.1804
Explanation:
We are given the following information in the question:
Mean customers enter the tellers’ queue every five minutes = 2
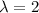
Thus, the number of customers that enter the tellers’ queue is Poisson distributed
Formula:
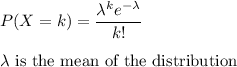
We have to evaluate:
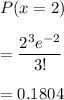
0.1804 is the probability that exactly three customers enter the queue in a randomly selected five-minute period.
Thus, the correct answer is
Option C) 0.1804