Question

A centrifuge in a medical laboratory rotates at an angular speed of 3,500 rev/min, clockwise (when viewed from above). When switched off, it rotates through 46.0 revolutions before coming to rest. Assuming it is constant, what is the magnitude of angular acceleration (in rad/s2)?

Answer 1

The magnitude of angular acceleration is
`232.38\ rad/s^2`.

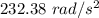Step-by-step explanation:

Given that,

Initial angular velocity,
`\omega_i=3500\ rev/min=366.5\ rad/s`

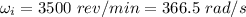
When it switched off, it comes o rest,
`\omega_f=0`

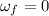
Number of revolution,
`\theta=46=289.02\ rad`

We need to find the magnitude of angular acceleration. It can be calculated using third equation of rotational kinematics as :

`\omega_f^2-\omega_i^2=2\alpha \theta\\\\\alpha =(-\omega_i^2)/(2\theta)\\\\\alpha =(-(366.51)^2)/(2* 289.02)\\\\\alpha =-232.38\ rad/s^2`

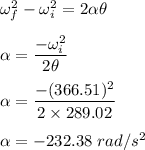
So, the magnitude of angular acceleration is
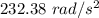`232.38\ rad/s^2`. Hence, this is the required solution.