Question

Jason states that Triangle A B C is congruent to triangle R S T. Kelley states that Triangle A B C is congruent to triangle T S R. Which best describes the accuracy of the congruency statements? On a coordinate plane, triangle A B C has points (2, 1), (3, 3), (4, 1). Triangle R S T has points (negative 4, negative 2), (negative 3, 0), (negative 2, negative 2). Jason's statement is correct. RST is the same orientation, shape, and size as ABC. Both statements could be correct. RST could be the result of two translations of ABC. TSR could be the result of a rotation and a translation of ABC. Both statements could be correct. RST could be the result of two translations of ABC. TSR could be the result of a reflection and a translation of ABC. Kelley's statement is correct. TSR is the same orientation, shape, and size as ABC.

Answer 1

Its A

Explanation:

Answer 2

The correct option is;

Jason's statement is correct. RST is the same orientation, shape, and size as ABC

Explanation:

Here we have

ABC = (2, 1), (3, 3), (4, 1)

RST = (-4, -2), (-3, 0), (-2, -2)

Therefore the length of the sides are as follows

AB =
`√((2-3)^2+(1-3)^2) = √(5)`

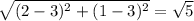
AC =
`√((2-4)^2+(1-1)^2) =2`

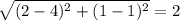
BC =
`√((3-4)^2+(3-1)^2) = √(5)`

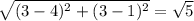
For triangle SRT we have

RS =
`√((-4-(-3))^2+(-2-0)^2) = √(5)`

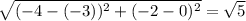
RT =
`√((-4-(-2))^2+(-2-(-2))^2) = 2`

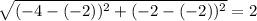
ST =
`√((-3-(-2))^2+(0-(-2))^2) = √(5)`

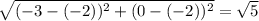
Therefore their dimensions are equal

However the side with length 2 occurs between (2, 1) and (4, 1) in triangle ABC and between (-4, -2) and (-2, -2) in triangle RST

That is Jason's statement is correct. RST is the same orientation, shape, and size as ABC.