Question

A double slit produces a diffraction pattern that is a combination of single and double slit interference. Find the ratio of the width of the slits (D) to the separation between them (d), if the second minimum of the single slit pattern falls on the sixth-order maximum of the double slit pattern. (This will greatly reduce the intensity of the sixth-order maximum. Assume the central maxima of the single slit and double slit interference patterns are located at the same place on the screen.)

Answer 1

To solve this problem we apply the concepts related to the concept of destructive interference. For the destructive interference for a single slit path difference is,

`dsin\theta = n\lambda`

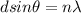
Where,

D = Slit width

n = Order of the minima

`\theta` = Angle relative to the original direction of the light

`\lambda` = Wavelength of the light

Now the first minima will have a n=1 then

`Dsin\theta_1 = 1\lambda`

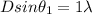
And the 5 order fringe will have n=5 then

`dsin\theta_2 = 5\lambda`

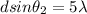
The ratio between the two variables will be

`(Dsin\theta_1)/(dsin\theta_5) = (\lambda)/(5\lambda)`

`(D)/(d) = (1)/(5)`

`d = 5D`

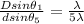
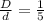
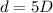
Therefore the slit separation is five times the slit width d=5D