Question

Linear functions can be used to find the price of a building based on its floor area below are two of these functions,

A. Find and compare the slopes

B. Find and compare the y-intercept

C. Describe each function as proportional or non proportion

Answer 1

Part A) see the explanation

Part B) see the explanation

Part C) see the explanation

Explanation:

The complete question in the attached figure

Part A) Find and compare the slopes

we have

Function 1

`y=40x+15,000`

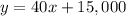
This is a linear equation in slope intercept form

`y=mx+b`

where

y is the price of the building in thousands

x is the floor area in square foot

m is the slope

b is the y-intercept

we have

`m=\$40\ per\ ft^2`

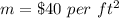
Function 2

we know that

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

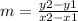
take two points from the data in the table

(400,32,000) and (700,56,000)

Remember that the price in the table is in thousands

substitute

`m=(56,000-32,000)/(700-400)`

`m=\$80\ per\ ft^2`

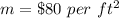
The slope of the Function 2 is greater than the slope of the Function 1

The slope of the Function 2 is two times the slope of the Function 1

Part B) Find and compare the y-intercept

we know that

The y-intercept is the value of y when the value of x is equal to zero

Function 1

`y=40x+15,000`

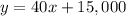
For x=0

`y=40(0)+15,000=\$15,000`

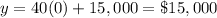
Function 2

Find the equation in point slope form

`y-y1=m(x-x1)`

we have

`m=80\\point\ (400,32,000)`

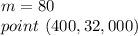
substitute

`y-32,000=80(x-400)`

Convert to slope intercept form

isolate the variable y

`y-32,000=80x-32,000\\y=80x`

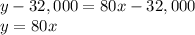
For x=0

`y=80(0)=0`

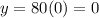
The y-intercept of the function 1 is $15,000 and the y-intercept of the function 2 is zero (the line passes through the origin)

Part C) Describe each function as proportional or non proportion

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
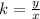`k=(y)/(x)` or
`y=kx`

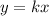
In a proportional relationship the constant of proportionality k is equal to the slope m of the line and the line passes through the origin

so

Function 1

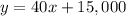`y=40x+15,000` -----> is a non proportional linear function (because the line has a y-intercept)

Function 2

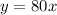`y=80x` ----> is a proportional linear equation (the line passes through the origin)