Question

I need help.....Which values are possible lengths for segments AC and CD, respectively?

Answer 1

Given:

Given that R is a circle.

The length of BC is 5 units.

The length of CE is 12 units.

We need to determine the lengths of AC and CD.

Length of the chord AD:

The lengths of the segments AC and CD can be determined using the intersecting chords theorem.

Applying the theorem, we have;

`AC \cdot CD=BC \cdot CE`

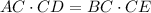
Substituting the values, we have;

`AC \cdot CD=5 * 12`

`AC \cdot CD=60`

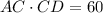
Hence, when multiplying the two segments AC and CD, we get 60 units.

Thus, the length of the chord AD is 60 units.

Option F: 6 and 10

The possible lengths of AC and CD can be determined by multiplying the two segments.

Thus, we have;

`AD=AC \cdot CD`

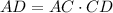
Substituting the values, we have;

`60=6 * 10`

`60=60`

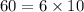
Thus, the possible lengths of AC and CD are 6 and 10 respectively.

Hence, Option F is the correct answer.

Option G: 8 and 9

Similarly, we have;

`AD=AC \cdot CD`

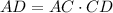
Substituting the values, we have;

`60=8 * 9`

`60 \\eq 72`

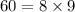
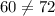
Since, both sides of the equation are not equal, Option G is not the correct answer.

Option H: 7 and 14

Similarly, we have;

`AD=AC \cdot CD`

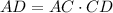
Substituting the values, we have;

`60=7 * 14`

`60 \\eq 98`

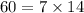
Since, both sides of the equation are not equal, Option H is not the correct answer.

Option J: 12 and 13

Similarly, we have;

`AD=AC \cdot CD`

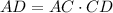
Substituting the values, we have;

`60=12 * 13`

`60 \\eq 156`

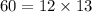
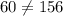
Since, both sides of the equation are not equal, Option J is not the correct answer.

Therefore, the possible lengths for segments AC and CD are 6 and 10 respectively.

Hence, Option F is the correct answer.