Question

The temperature of a certain solution is estimated by taking a large number of independent measurements and averaging them. The estimate is 37◦C, and the uncertainty (standard deviation) in this estimate is 0.1 ◦C. (a) Find a 95% confidence interval for the temperature. (b) What is the confidence level of the interval 37 ± 0.1 ◦C? (c) If only a small number of independent measurements had been made, what additional assumption would be necessary in order to compute a confidence interval? (d) Making the additional assumption, compute a 95% confidence interval for the temperature if 10 measurements were made.

Answer 1

(a) The 95% confidence interval for the temperature is (36.80°C, 37.20°C).

(b) The confidence level is 68%.

(c) The necessary assumption is that the population is normally distributed.

(d) The 95% confidence interval for the temperature if 10 measurements were made is (36.93°C, 37.07°C).

Explanation:

Let X = temperature of a certain solution.

The estimated mean temperature is,
`\bar x=37^(o)C`.

The estimated standard deviation is,
`s=0.1^(o)C`.

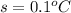(a)

The general form of a (1 - α)% confidence interval is:

`CI=SS\pm CV* SD`

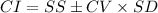
Here,

SS = sample statistic

CV = critical value

SD = standard deviation

It is provided that a large number of independent measurements are taken to estimate the mean and standard deviation.

Since the sample size is large use a z-confidence interval.

The critical value of z for 95% confidence interval is:

`z_(0.025)=1.96`

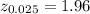
Compute the confidence interval as follows:

`CI=SS\pm CV* SD\\=37\pm 1.96* 0.1\\=37\pm0.196\\=(36.804, 37.196)\\\approx (36.80^(o)C, 37.20^(o)C)`

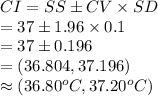
Thus, the 95% confidence interval for the temperature is (36.80°C, 37.20°C).

(b)

The confidence interval is, 37 ± 0.1°C.

Comparing the confidence interval with the general form:

`37\pm 0.1=SS\pm CV* SD`

The critical value is,

CV = 1

Compute the value of P (-1 < Z < 1) as follows:

`P(-1<Z<1)=-P(Z<-1)\\=P(Z<1)-[1-P(Z<1)]\\=2P(Z<1)-1\\=(2* 0.8413)-1\\=1.6826-1\\=0.6826\\\approx0.68`

The percentage of z-distribution between -1 and 1 is, 68%.

Thus, the confidence level is 68%.

(c)

The confidence interval for population mean can be constructed using either the z-interval or t-interval.

If the sample selected is small and the standard deviation is estimated from the sample, then a t-interval will be used to construct the confidence interval.

But this will be possible only if we assume that the population from which the sample is selected is Normally distributed.

Thus, the necessary assumption is that the population is normally distributed.

(d)

For n = 10 compute a 95% confidence interval for the temperature as follows:

The (1 - α)% t-confidence interval is:

`CI=\bar x\pm t_(\alpha/2, (n-1))* (s)/(√(n))`

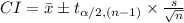
The critical value of t is:

`t_(\alpha/2, (n-1))=t_(0.025, 9)=2.262`

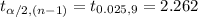
*Use a t-table for the critical value.

The 95% confidence interval is:

`CI=37\pm 2.262* (0.1)/(√(10))\\=37\pm 0.072\\=(36.928, 37.072)\\\approx (36.93^(o)C, 37.07^(o)C)`

Thus, the 95% confidence interval for the temperature if 10 measurements were made is (36.93°C, 37.07°C).