Question

ANSWER THIS PLEASE ASAP

Answer 1

Answer: a.) 72 of each type of animal, for a total of 216

b.) 16 grown cats, 4 kittens

Step-by-step explanation:

part a. It's a distribution (division) problem. The same number of each animal is distributed over some unknown number of troughs, but the total number of troughs adds up to 69. ( I hate to give this all away, as its a brilliant problem! )

Number of troughs for each animal type is How many needed by the number of animals per trough:

h/2 + c/3 + p/8 = 69

Since we are given "the same number of horses, cows and pigs" we can substitute "x" for all.

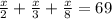`(x)/(2) + (x)/(3) +(x)/(8) = 69` Get a common denominator. 24 would work, 48 also.

`48((x)/(2) +(x)/(3) +(x)/(8) ) = 48(69)`

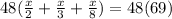
24x + 16x + 6x = 3372

46x = 3372 x = 72

Proof: calculate the number of each kind of trough

Horses 72/2 = 36, Cows 72/3 = 24 Pigs 72/8 = 9 36+24+9 = 69

part b. 5c + 3k = 92, c + k = 20 Rearrange to get a value for c to substitute.

c = 20-k 5(20-k) +3k =92 Distribute and solve

100 - 5k + 3k = 92 becomes -2k = -8 so k = 4 Substitute into the original

c + 4 = 20 becomes c=20-4, so c = 16

Proof: 5c +3k = 92 Substitute values 5(16) + 3(4) = 92 80 + 12 = 92