Answer:
Mass,

Step-by-step explanation:
Charge of the ionized particle is +1 e
Uniform magnetic field, B = 1.6 T
The particle enters the magnetic field such that its velocity is perpendicular to the magnetic field.
Radius of circle, r = 2 cm = 0.02 m
Time, t = 0.56 μs
We need to find the mass of the particle. We know that when object moves in magnetic field, centripetal force balances its motion. So,
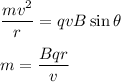 .......(1)
.......(1)
v is velocity of particle
Velocity,
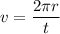
So, equation (1) becomes :
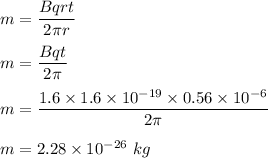
So, the mass of the particle is
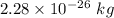 .
.