Question

You have a stopped pipe of adjustable length close to a taut 85.0cm, 7.25g wire under a tension of 4170N. You want to adjust the length of the pipe so that, when it produces sound at its fundamental frequency , this sound causes the wire to vibrate in its second overtone (third harmonic). With a very large amplitude. How long should the pipe be?

Answer 1

The length is
`L_d= 0.069 \ m`

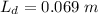
Step-by-step explanation:

From the question we are told that

The length of the wire
`L = 85cm = (85)/(100) = 0.85m`

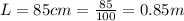
The mass is
`m = 7.25g = (7.25)/(1000) = 7.25^10^(-3)kg`

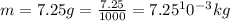
The tension is
`T = 4170N`

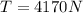
Generally the frequency of oscillation of a stretched wire is mathematically represented as

`f = (n)/(2L) \sqrt{(T)/(\mu)`

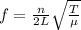
Where n is the the number of nodes = 3 (i.e the third harmonic)

`\mu` is the linear mass density of the wire

This linear mass density is mathematically represented as

`\mu = (m)/(L)`

Substituting values

`\mu = (7.2*10^(-3))/(0.85)`

`= 8.53 *10^(-3) kg/m`

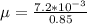
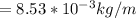
Substituting values in to the equation for frequency

`f = (3)/(2 80.85) * \sqrt{(4170)/(8.53*10^(-3)) }`

`= 1234Hz`

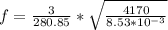
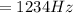
From the question the we can deduce that the fundamental frequency is equal to the oscillation of a stretched wire

The fundamental frequency is mathematically represented as

`f = (v)/(4L_d)`

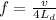
Where
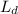`L_d` is the length of the pipe

v is the speed of sound with a value of
`v = 343m/s`

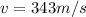
Making
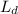`L_d` the subject of the formula

`L_d = (v)/(4f)`

Substituting values

`L_d = (343)/((4)(1234))`

`L_d= 0.069 \ m`

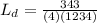
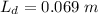
From the question the we can deduce that the fundamental frequency is equal to the oscillation of a stretched wire