Question

The endpoints of directed line segment PQ have coordinates of P(-7,5) and Q(5,3). What are the coordinates of point A, on PQ, that divide PQ into a ratio of 1:3?

Answer 1

Correction

P(-7,-5)

Answer:

d(-4,-3)

Explanation:

-Given the coordinates of PQ as P(-7,5) and Q(5,3).

-The sum of the ratios is:

`\sum(ratios)=1+3\\\\=4`

Let d be the point that divide's the segment in the ratio 1:3

#The coordinates that divide the segment into a 1:3 ratio therefore has to be
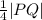`(1)/(4)|PQ|` from P.

#We determine the length of the x-axis coordinate:

`|PQ|_x=Q_x-P_x\\\\=5--7\\\\=12\\\\\therefore d_x=-7+(1)/(4)* 12\\\\=-4`

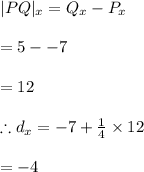
#We determine the length of the y-axis coordinate:

`|PQ|_y=Q_y-P_y\\\\=3--5\\\\=8\\\\\therefore d_y=-5+(1)/(4)* 8\\\\=-3`

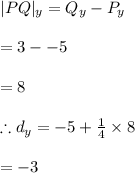
Hence, the coordinates of point d is d(-4,-3)