Question

A coin is resting on the bottom of an empty container. The container is then filled to the brim three times, each time with a different liquid. An observer (in air) is directly above the coin and looks down at it. With liquid A in the container, the apparent depth of the coin is 7 cm, with liquid B it is 6 cm, and with liquid C it is 5 cm. Rank the indices of refraction of the liquids in descending order (largest first).

Answer 1

Refractive index of liquid C > Refractive index of liquid B > Refractive index of liquid A

Step-by-step explanation:

Let the depth of each section is h.

That means the real depth for each section is h.

Apparent depth is liquid A is 7 cm.

Apparent depth in liquid B is 6 cm.

Apparent depth in liquid C is 5 cm.

by the formula of the refractive index

n = real depth / apparent depth

where, n is the refractive index of the liquid.

For liquid A:

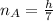`n_(A)=(h)/(7)` .... (1)

For liquid B:

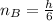`n_(B)=(h)/(6)` ..... (2)

For liquid C:

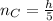`n_(C)=(h)/(5)` ..... (3)

By comparing all the three equations

nc > nB > nA

Refractive index of liquid C > Refractive index of liquid B > Refractive index of liquid A