Question

A company employs two shifts of workers. Each shift produces a type of gasket where the thickness is the critical dimension. The average thickness and the standard deviation of thickness for shift 1, based on a random sample of 40 gaskets, are 10.85 mm and 0.16 mm, respectively. The similar figures for shift 2, based on a random sample of 30 gaskets, are 10.90 mm and 0.19 mm. Let µ1-µ2 be the difference in thickness between shifts 1 and 2, and assume that the population variances are equal.

(a) Find a 95% confidence interval for µ1-µ2.
(b) Based on your answer to part a, are you convinced that the gaskets from
shift 2 are, on average, wider than those from shift 1? Why or why not?
(c) How would your answers to parts a and b change if the sample sizes
were instead 300 and 250?

Answer 1

a)
`[-0.134,0.034]`

b) We are uncertain

c) It will change significantly

Explanation:

a) Since the variances are unknown, we use the t-test with 95% confidence interval, that is the significance level = 1-0.05 = 0.025.

Since we assume that the variances are equal, we use the pooled variance given as

`s_p^2 = ( (n_1 -1)s_1^2 + (n_2-1)s_2^2)/(n_1+n_2-2)`,

where
`n_1 = 40, n_2 = 30, s_1 = 0.16, s_2 = 0.19`.

The mean difference
`\mu_1 - \mu_2 = 10.85 - 10.90 = -0.05`.

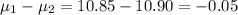The confidence interval is

`(\mu_1 - \mu_2) \pm t_(n_1+n_2-2,\alpha/2) \sqrt{(s_p^2)/(n_1) + (s_p^2)/(n_2)} = (-0.05) \pm t_(68,0.025) \sqrt{(0.03)/(40) + (0.03)/(30)}`

`= -0.05\pm 1.995 * 0.042 = -0.05 \pm 0.084 = [-0.134,0.034]`

b) With 95% confidence, we can say that it is possible that the gaskets from shift 2 are, on average, wider than the gaskets from shift 1, because the mean difference extends to the negative interval or that the gaskets from shift 1 are wider, because the confidence interval extends to the positive interval.

c) Increasing the sample sizes results in a smaller margin of error, which gives us a narrower confidence interval, thus giving us a good idea of what the true mean difference is.