Question

Two disks are rotating about the same axis Disk A has a moment of inertia of 4.11 kg m2 and an angular velocity of 9.06 rad s Disk B is rotating with an angular velocity of 8.24 rad s The two disks are then linked together without the aid of any external torques so that they rotate as a single unit with an angular velocity of 2.18 rad s The axis of rotation for this unit is the same as that for the separate disks What is the moment of inertia of disk B

Answer 1

4.66kgm^2

Step-by-step explanation:

The total rotational kinetic energy of both disks must conserve. Hence, we have:

`E_k=(1)/(2)(I_A+I_B)\omega^2=(1)/(2)I_A\omega_A^2+(1)/(2)I_B\omega_B^2`

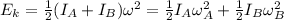
where w is the angular velocity when both disks are stick together, wA nad wB are the angular velocities when the disks are apart and IA and IB are the moment of inertia respectively.

By taking apart wB and replacing we obtain:

`I_B(\omega^2-\omega_B^2)=I_A(\omega_A^2-\omega^2)\\\\I_B=(I_A(\omega_A^2-\omega^2))/(\omega^2-\omega_B^2)=(4.11kgm^2[(9.06(rad)/(s))^2-(2.18(rad)/(s))^2])/((2.18(rad)/(s))-(8.24(rad)/(s)))=-4.66kgm^2`

hope this helps!!