Answer:
The smallest angle formed by the trenches is 26° and
The area of the plot of land within the trenches to the nearest foot is;
33443 ft²
Explanation:
Here we have the firefighters made a triangular shape out of trenches surrounding the fire
The lengths of the sides of the triangle formed is given as
250 ft, 312 ft and 490 ft
We are required to find, to the nearest degree, the smallest angle formed by the trenches
We note that the smallest angle is subtended by the shortest length of the trench which is 250 ft.
Therefore,
From cosine relations, we have
a² = b² + c² - 2·b·c·cos (α)
Which gives,
250² = 312² + 490² - 2×312×490×cos (α)
cos (α) = 0.8992
cos (0.8992)⁻¹ = 25.95° ≈ 26°
The area is given by
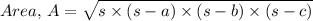
Where:
a, b, c are the lengths of the sides of the triangle and
s = Half the perimeter of the triangle, that us (a + b + c)/2
We put a = 250, b = 312 and c = 490
Therefore s = (250 + 312 + 490)/2 = 526
Therefore,
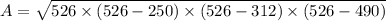
= 33443.025 ft² ≈ 33443 ft².