Question

According to a study conducted by ABODO, about 70% of all college students use an online dating app. Suppose you want to know if Ohio State students are similar to their national peers. You ask a random sample of 125 OSU students and find that 78 of them use an online dating app. a. Does this sample provide significant evidence at the ???? = .05 level that the true proportion of OSU students that use an online dating app is different than the ABODO estimate? Conduct a hypothesis test to justify your answer.

Answer 1

There is no enough evidence to claim that the true proportion of OSU students that use an online dating app is different than the ABODO estimate.

Explanation:

We have to perform a hypothesis test on a proportion.

The null hypotesis will state that the proportion of students of Ohio State that use dating apps is equal to the college students proportion (p=0.7).

The alternative hypothesis will state that these proportions differ.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.7\\\\H_a:\pi\\eq0.7`

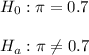
The test is two-tailed. The significance level is 0.05.

The sample size is n=125.

Out of 125 students, 78 of them use an online dating app, so the sample proportion is:

`p=78/125=0.624`

The standard error is calculated as:

`\sigma_p=\sqrt(\pi(1-\pi))/(N)}=\sqrt(0.7*0.3)/(125)}=√(0.00168)=0.041`

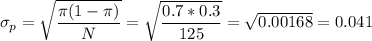
We can now calculate the test statistic

`z=(p-\pi+0.5/N)/(\sigma_p)=(0.624-0.7+0.004)/(0.041)=(-0.072)/(0.041)=-1.756`

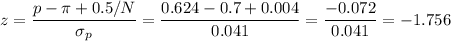
As it is a two-side test, the P-value for this statistic can be calculated as:

`P-value=2*P(z<-1.756)=0.08`

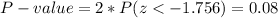
The P-value is bigger than the significance level, so the effect is not significant. The null hypothesis is failed to be rejected.

There is no enough evidence to claim that the true proportion of OSU students that use an online dating app is different than the ABODO estimate.