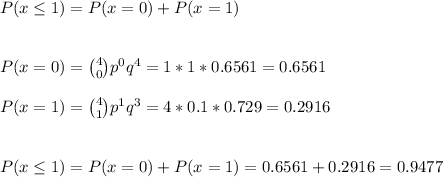Question

It is known that 10% of the calculators shipped from a particular factory are defective. What is the probability that no more than one in a random sample of four calculators is defective? Multiple Choice 0.2916 0.9477 0.3439 0.6561

Answer 1

The probability that no more than one in a random sample of four calculators is defective is 0.9477.

Explanation:

We can model this as a binomial randome variable, because we have a sum of n Bernoulli variables with probability p of success.

In this case, the sample size is n=4 and the probability of an individual defective calculator is p=0.10.

The probability of having k defective calculators in a sample of n calculators is calculated as:

`P(x=k)=\binom{n}{k}p^k(1-p)^(n-k)`

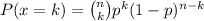
We have to calculate the probability that no more than one out of four calculators is defective (P(x≤1)). This is the same as adding the probability of having no defective calculator in the sample (P(x=0)) and the probabiltity of having one defective in the sample (P(x=1)):

`P(x\leq 1)=P(x=0)+P(x=1)\\\\\\P(x=0) = \binom{4}{0} p^(0)q^(4)=1*1*0.6561=0.6561\\\\P(x=1) = \binom{4}{1} p^(1)q^(3)=4*0.1*0.729=0.2916\\\\\\P(x\leq 1)=P(x=0)+P(x=1)=0.6561+0.2916=0.9477`