Question

Mercury levels were collected on 43 random specimens of Albacore tuna, the average mercury levels was found to be 0.358 parts per million (ppm) and the standard deviation of mercury level was 0.138 (ppm). The FDA website reports that the average mercury level in all Albacore tuna is 0.391 ppm. The researchers wish to know if the average mercury level in Albacore tuna is different from what is reported on the FDA website. Test the hypothesis at 5% level of significance. Calculate the p-value to perform the test at 5% level of significance. (Hint: p-value is dependent on the direction of the alternative and the test statistic value)

Answer 1

We conclude that the average mercury level in Albacore tuna is same as reported on the FDA website.

Explanation:

We are given that Mercury levels were collected on 43 random specimens of Albacore tuna, the average mercury levels was found to be 0.358 parts per million (ppm) and the standard deviation of mercury level was 0.138 (ppm).

The FDA website reports that the average mercury level in all Albacore tuna is 0.391 ppm.

Let
`\mu` = average mercury level in all Albacore tuna

SO, Null Hypothesis,
`H_0` :
`\mu` = 0.391 ppm {means that the average mercury level in Albacore tuna is same as reported on the FDA website}

Alternate Hypothesis,
`H_A` :
`\mu`
`\\eq` 0.391 ppm {means that the average mercury level in Albacore tuna is different from what is reported on the FDA website}

The test statistics that will be used here is One-sample t test statistics because we don't know about the population standard deviation;

T.S. =
`\frac{\bar X -\mu}{{(s)/(√(n) ) } }` ~
`t_n_-_1`

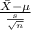where,
`\mu` = sample average mercury levels = 0.358 ppm

s = sample standard deviation = 0.138 ppm

n = sample of specimens = 43

So, test statistics =
`\frac{0.358-0.391}{{(0.138)/(√(43) ) } }` ~
`t_4_2`

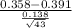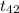
= -1.568

Now at 0.05 significance level, the t table gives critical values between -2.0186 and 2.0186 at 42 degree of freedom for two-tailed test. Since our test statistics lies within the range of critical values of t so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Now, P-value of the test statistics is given by;

P-value = P(
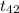`t_4_2` > -1.568) = 0.065 or 6.5%

• If the P-value of test statistics is more than the level of significance, then we will not reject our null hypothesis as it will not fall in the rejection region.

• If the P-value of test statistics is less than the level of significance, then we will reject our null hypothesis as it will fall in the rejection region.

Now, here the P-value is 0.065 which is clearly higher than the level of significance of 0.05, so we will not reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the average mercury level in Albacore tuna is same as reported on the FDA website.