Answer:
0.021
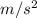
Step-by-step explanation:
The period of a pendulum is dependent on the length of the string holding the pendulum, L, and acceleration due to gravity, g. It is given mathematically as:
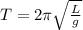
Let us make L the subject of the formula:
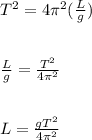
We are not told that the length of the string changes, hence, we can conclude that it is constant in both locations.
When the period of the pendulum is 2 s and the acceleration due to gravity is 9.8
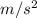 , the length L is:
, the length L is:
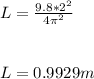
When the pendulum is moved to a new location, the period becomes 1.99782 s.
We have concluded that length is constant, hence, we can find the new acceleration due to gravity,
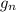 :
:
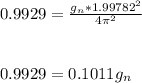
Therefore:

The difference between the new acceleration due to gravity,
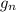 and the former acceleration due to gravity, g, will be:
and the former acceleration due to gravity, g, will be:
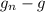 =
=
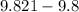 =
=
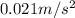
The acceleration due to gravity differs by a value of
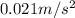 at the new location.
at the new location.