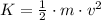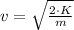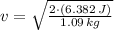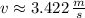Answer:
a)
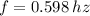 , b)
, b)
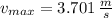 , c)
, c)
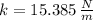 , d)
, d)
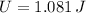 , e)
, e)
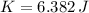 , f)
, f)
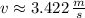
Step-by-step explanation:
a) The frequency of oscillation is:
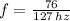
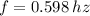
b) The angular frequency is:
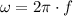
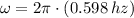
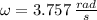
Lastly, the speed at the equilibrium position is:
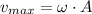
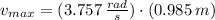
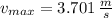
c) The spring constant is:
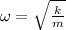
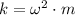
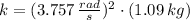
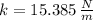
d) The potential energy when the particle is located 38.1 % of the amplitude away from the equilibrium position is:
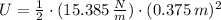
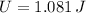
e) The maximum potential energy is:
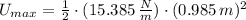
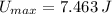
The kinetic energy when the particle is located 38.1 % of the amplitude away from the equilibrium position is:
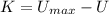
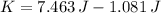
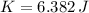
f) The speed when the particle is located 38.1 % of the amplitude away from the equilibrium position is: