Question

Laser scientists can now generate pulses of light as short as 1 fs = 10−15 s. One of the great difficulties in working with such short pulses is that many EM waves of different frequencies must be superposed to create the pulse. Because real optical elements like lenses and prisms are made of real materials for which the index of refraction is wavelengthdependent i.e., the material is dispersive, parts of the pulse with different frequencies travel through the optical elements at different speeds and become separated, so the pulse spreads out. Consider a short laser pulse which is normally incident on a piece of crown glass which is L = 3.39 mm thick. The index of refraction for a wavelength of λB = 402 nm in the blue part of the pulse is nB = 1.53, and the index of refraction for a wavelength of λR = 672 nm in the red part of the pulse is nR = 1.51. How much sooner does the red part of the pulse arrive at the end of the piece of glass than the blue part? Answer in units of fs.

Answer 1

Δt =2.3 10² fs

Step-by-step explanation:

For this exercise we use that the speed of a wave or a pulse is constant in a material medium, therefore we can use the kinematic relations of the uniform movement

v = d / t

t = d / v

also the refractive index is

n = c / v

v = c / n

where c is the speed of light in a vacuum that is 2.998 108 m / s

we substitute

t = d n / c

we apply this equation to our case

We reduce the magnitudes to the SI system

d = 3.39 mm = 3.39 10⁻³ m

first wavelength

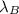`\lambda _(B)` = 402 nm

`n_(B)` = 1.53

`t_(B)` = 3.39 10⁻³ 1.53 / 2,998 10⁸

t_{B} = 1.73 10⁻¹¹ s

we reduce to fentoseconds

t_{B} = 1.73 10⁻¹¹ s (1 10¹⁵ fs / 1 s)

t_{B} = 1,730 10⁴ fs

second wavelength

\lambda _{R} = 672 nm

n_{R} = 1.51

t_{R} = 3.39 10⁻³ 1.51 / 2,998 10⁸

t_{R} = 1,707 10⁻¹¹ s

t_{R} = 1,707 10⁴ fs

the time difference between the two pulses is

Δt = t_{B} - t_{R}

Δt = (1.730 -1.707 ) 10⁴ fs

Δt =2.3 10² fs