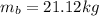Complete Question
The diagram for this question is shown on the first uploaded image
Answer:
The mass of the boom is
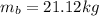
Step-by-step explanation:
From the question we are told that
The mass is

The tension the cable is
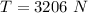
A sketch of the free body diagram is shown on the second uploaded image
From the second diagram
The length L is evaluated as

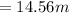
The angle
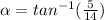 s
s
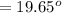
The angle
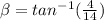
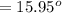
At equilibrium the net torque about x is zero and this can be represented mathematically
![T * sin (\alpha + \beta ) * L -[(m_bg )/(2) +mg ]* L cos \beta = 0](https://img.qammunity.org/2021/formulas/physics/college/3h0qanagbtizycbuz9pyx39zbdck06o53p.png)
![T * sin (\alpha + \beta ) * L = [(m_bg )/(2) +mg ]* L cos \beta](https://img.qammunity.org/2021/formulas/physics/college/1l1quy9cq31xld50d2rrifp1r3sck0bck4.png)
Where g is the acceleration due to gravity with a value of
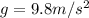
Making
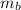 the mass of the boom the subject of the formula
the mass of the boom the subject of the formula
![m_b = (2 *[(T sin(\alpha +\beta ) )/(cos \beta ) -mg])/(g)](https://img.qammunity.org/2021/formulas/physics/college/y6com81a8tiy7vzttbbbaujo26lx13tbl8.png)
Substitution the values
![m_b = (2 *[(3206 * sin (19.65 + 15.95))/(cos 15.95) - 187.5*9.8])/(9.8)](https://img.qammunity.org/2021/formulas/physics/college/88zpquuylibxz207iq3dr5yie2lxgwpcul.png)