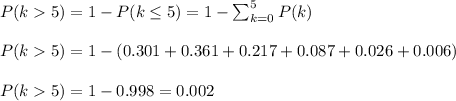Question

A pen company averages 1.2 defective pens per carton produced (200 pens). The number of defects per carton is Poisson distributed. a. What is the probability of selecting a carton and finding no defective pens? b. What is the probability of finding eight or more defective pens in a carton? c. Suppose a purchaser of these pens will quit buying from the company if a carton contains more than five defective pens. What is the probability that a carton contains more than five defective pens? P(x = 0 | λ = 1.2) = b. P(x ≥ 8 | λ = 1.2) = c. P(x > 5 | λ = 1.2) =

Answer 1

a. P(x = 0 | λ = 1.2) = 0.301

b. P(x ≥ 8 | λ = 1.2) = 0.000

c. P(x > 5 | λ = 1.2) = 0.002

Explanation:

If the number of defects per carton is Poisson distributed, with parameter 1.2 pens/carton, we can model the probability of k defects as:

`P(k)=(\lambda^(k)e^(-\lambda))/(k!)= (1.2^(k)\cdot e^(-1.2))/(k!)`

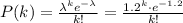
a. What is the probability of selecting a carton and finding no defective pens?

This happens for k=0, so the probability is:

`P(0)=(1.2^(0)\cdot e^(-1.2))/(0!)=e^(-1.2)=0.301`

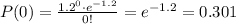
b. What is the probability of finding eight or more defective pens in a carton?

This can be calculated as one minus the probablity of having 7 or less defective pens.

`P(k\geq8)=1-P(k<8)=1-\sum_(k=0)^7P(k)=1-\sum_(k=0)^7 (1.2^(k)\cdot e^(-1.2))/(k!)`

`P(0)=1.2^(0) \cdot e^(-1.2)/0!=1*0.3012/1=0.301\\\\P(1)=1.2^(1) \cdot e^(-1.2)/1!=1*0.3012/1=0.361\\\\P(2)=1.2^(2) \cdot e^(-1.2)/2!=1*0.3012/2=0.217\\\\P(3)=1.2^(3) \cdot e^(-1.2)/3!=2*0.3012/6=0.087\\\\P(4)=1.2^(4) \cdot e^(-1.2)/4!=2*0.3012/24=0.026\\\\P(5)=1.2^(5) \cdot e^(-1.2)/5!=2*0.3012/120=0.006\\\\P(6)=1.2^(6) \cdot e^(-1.2)/6!=3*0.3012/720=0.001\\\\P(7)=1.2^(7) \cdot e^(-1.2)/7!=4*0.3012/5040=0\\\\`

`P(k<8)=\sum_(k=0)^7P(k)\\\\P(k<8)=0.301+0.361+0.217+0.087+0.026+0.006+0.001+0\approx1\\\\\\P(k\geq8)=1-P(k<8)=1-1=0`

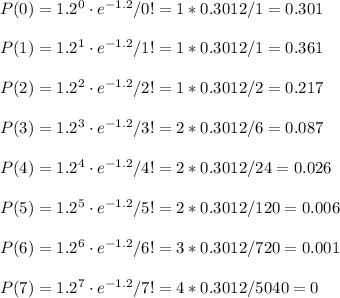
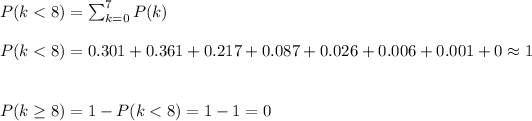
c. Suppose a purchaser of these pens will quit buying from the company if a carton contains more than five defective pens. What is the probability that a carton contains more than five defective pens?

We can calculate this as we did the previous question, but for k=5.

`P(k>5)=1-P(k\leq5)=1-\sum_(k=0)^5P(k)\\\\P(k>5)=1-(0.301+0.361+0.217+0.087+0.026+0.006)\\\\P(k>5)=1-0.998=0.002`