Question

An object is thrown with velocity v from the edge of a cliff above level ground. Neglect air resistance. In order for the object to travel a maximum horizontal distance from the cliff before hitting the ground, the throw should be at an angle θ with respect to the horizontal of:________.

(A) greater than 60° above the horizontal
(B) greater than 45° but less than 60° above the horizontal
(C) greater than zero but less than 45° above the horizontal
(D) zero
(E) greater than zero but less than 45° below the horizontal

Answer 1

The correct option is;(C) greater than zero but less than 45° above the horizontal

Step-by-step explanation:

Here, we have for maximum horizontal distance

h = v×t

Where t is the time of flight

The time of flight is given by

s = v·t - 0.5 × gt² to maximize the time of flight, we therefore increase the height such that

Since the range is given by

Horizontal range, x = v·t·cosα

Vertical range, y = v·t·sinα - 0.5·g·t²

When the particle comes back to initial level, we have

0 = v·t·sinα - 0.5·g·t² → 0 = t(v·sinα - 0.5·g·t)

So that t = 0 or t =
`(2\cdot v\cdot sin\alpha )/(g)`

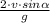
Therefore, horizontal range =

`(v^(2) \cdot 2\cdot cos\alpha \cdot sin\alpha )/(g) = (v^2sin(2\alpha) )/(g)`

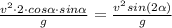
Therefore maximum range is obtained when α = 45° as sin 90° = 1

Answer 2

(C) greater than zero but less than 45° above the horizontal

Step-by-step explanation:

The range of a projectile is given by R = v²sin2θ/g.

For maximum range, sin2θ = 1 ⇒ 2θ = sin⁻¹(1) = 90°

2θ = 90°

θ = 90°/2 = 45°

So the maximum horizontal distance R is in the range 0 < θ < 45°, if θ is the angle above the horizontal.