Question

A 1600 kg car moving south at 11.0 m/s collides with a 2700 kg car moving north. The cars stick together and move as a unit after the collision at a velocity of 5.08 m/s to the north.

A) Find the velocity of the 2700 kg car before the collision.

Answer 1

U = 14.61 m/s

Step-by-step explanation:

Parameters given:

Mass of first car, m = 1600 kg

Initial velocity of first car, u = -11.0 m/s

(Taking the South as the negative y axis and the North as the positive y axis)

Mass of second car, M = 2700 kg

Initial velocity of second car, U is unknown

Final velocity of both cars, v = 5.08 m/s

To find the initial velocity of the first car, we apply the law of conservation of momentum:

Total initial momentum = Total final momentum

`mu + MU = mv + Mv\\\\\\mu + MU = (m + M)v`

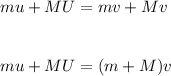
Inputting the values of m, M, u and v:

`(1600 * -11) + (2700 * U) = (1600 + 2700) * 5.08\\\\\\-17600 + 2700U = 21844\\\\\\2700U = 21844 + 17600\\\\\\2700U = 39444\\\\\\U = 39444/2700\\\\\\U = 14.61 m/s`

The initial velocity of the 2700 kg car is 14.61 m/s.