Question

A random sample of 18 young adult men (20 – 30 years old) was sampled. Each person was asked how many minutes of sports he watched on television daily. The responses are listed here. It is known that the standard deviation is 10.

Test to determine at the 5% significance level whether there is enough statistical evidence to infer that the mean amount of television watched daily by all young adult men is greater than 50 minutes.A random sample of 18 young adult men (20 – 30 years old) was sampled. Each person was asked how many minutes of sports he watched on television daily. The responses are listed here. It is known that the standard deviation is 10.
Test to determine at the 5% significance level whether there is enough statistical evidence to infer that the mean amount of television watched daily by all young adult men is greater than 50 minutes.

50 48 65 74 66 37 45 68 64
65 58 55 52 63 59 57 74 65

Answer 1

There is enough evidence to claim that the mean amount of television watched daily by all young adult men is greater than 50 minutes.

Explanation:

We have a sample of size n=18. The sample is: [50 48 65 74 66 37 45 68 64

65 58 55 52 63 59 57 74 65]

The mean of this sample is

`\bar x=(1)/(n) \sum_(i=1)^(18)x_i=59.17`

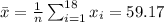
The population standard deviation is known and is

`\sigma=10`

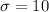
The null and alternative hypothesis are:

`H_0: \mu\leq50\\\\H_a: \mu>50`

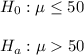
The significance level is

`\alpha=0.05`

The z-statistic is

`z=(\bar x-\mu)/(\sigma/√(n))=(59.17-50)/(10/√(18))=(9.17)/(2.357)=3.89`

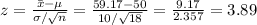
The P-value for this z-statistic is:

`P(x>3.89)=0.00005`

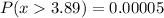
As the P-value is smaller than the significance level, the effect is significant. The null hypothesis is rejected.

There is enough evidence to claim that the mean amount of television watched daily by all young adult men is greater than 50 minutes.