Question

A small wooden block with mass 0.750 kg is suspended from the lower end of a light cord that is 1.72 m long. The block is initially at rest. A bullet with mass 0.0100 kg is fired at the block with a horizontal velocity v0. The bullet strikes the block and becomes embedded in it. After the collision the combined object swings on the end of the cord. When the block has risen a vertical height of 0.800 m, the tension in the cord is 4.86 N.

What was the initial speed v0 of the bullet?

Answer 1

`v_(0)=319.2 m/s`

Step-by-step explanation:

We need to use the momentum and energy conservation.

`p_(0)}=p_(f)`

`mv_(0)=(m+M)V_(1)`

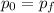
Where:

• m is the mass of bullet (m=0.01 kg)
• M is the mass of the wooden (M=0.75 kg)
• v(0) initial velocity of bullet
• V(1) is the velocity of the combined object in the moment the bullet hist the block

Conservation of energy.

We have kinetic energy at first and kinetic and potential energy at the end.

`(1/2)(m+M)V_(1)^(2)=(1/2)(m+M)V_(2)^(2)+(m+M)gh`

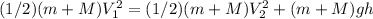
Here:

• V(1) is the velocity of the combined at the initial position
• h is the vertical height ( h = 0.800 m)

We can find V(2) using the definition of force at this point:

`\Sigma F=(m+M)a_(c)=(m+M)(V_(2)^(2)/R)`

`T-(m+M)gcos(\theta)=(m+M)a_(c)=(m+M)(V_(2)^(2)/R)`

`cos(\theta) =(L-h)/L=(1.72-0.8)/1.72`

`\theta =57.66`

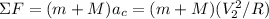
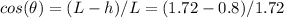
Now, we can solve the equation to find V(2)

`V_(2)=\sqrt{(R*(T-(m+M)*g*cos(\theta)))/((m+M))}`

`V_(2)=\sqrt{(1.72*(4.86-(0.01+0.75)*9.81*cos(57.66)))/((0.01+0.75))}`

`V_(2)=1.40 m/s`

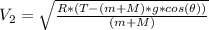
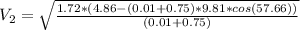
Now we can find V(1) using the conservation of energy equation

`(1/2)V_(1)^(2)=(1/2)V_(2)^(2)+gh`

`V_(1)=\sqrt{V_(2)^(2)+2gh}`

`V_(1)=\sqrt{1.40^(2)+2*9.81*0.8}`

`V_(1)=4.20 m/s`

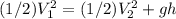
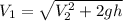
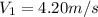
Finally, using the momentum equation we find v(0)

`v_(0)=((m+M)V_(1))/(m)`

`v_(0)=((0.01+0.75)*4.20)/(0.01)`

`v_(0)=319.2 m/s`

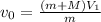
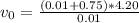
I hope it helps you!