Answer:
a)
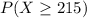
b) 7.35% probability that at least 215 of the 400 watches are defective.
Explanation:
I am going to use the binomial approximation to the normal to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
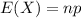
The standard deviation of the binomial distribution is:
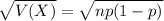
Normal probability distribution
Problems of normally distributed samples can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that
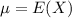 ,
,
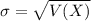 .
.
In this problem, we have that:
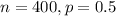
So
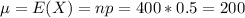
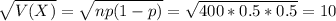
(a) Write an expression for the exact probability that at least 215 of the 400 watches are defective.
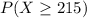
(b) Approximate the probability, using either the Poisson or normal approximation, whichever is appropriate, that at least 215 of the 400 watches are defective.
Using continuity correction, this is
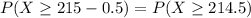 , which is 1 subtracted by the pvalue of Z when X = 214.5. So
, which is 1 subtracted by the pvalue of Z when X = 214.5. So

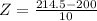
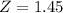
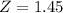 has a pvalue of 0.9265
has a pvalue of 0.9265
1 - 0.9265 = 0.0735
7.35% probability that at least 215 of the 400 watches are defective.