Answer:
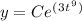
Explanation:
Beginning with the first differential equation:
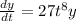
This differential equation is denoted as a separable differential equation due to us having the ability to separate the variables. Divide both sides by 'y' to get:
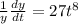
Multiply both sides by 'dt' to get:
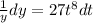
Integrate both sides. Both sides will produce an integration constant, but I will merge them together into a single integration constant on the right side:


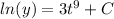
We want to cancel the natural log in order to isolate our function 'y'. We can do this by using 'e' since it is the inverse of the natural log:
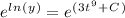
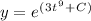
We can take out the 'C' of the exponential using a rule of exponents. Addition in an exponent can be broken up into a product of their bases:
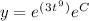
The term e^C is just another constant, so with impunity, I can absorb everything into a single constant:
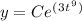
To check the answer by differentiation, you require the chain rule. Differentiating an exponential gives back the exponential, but you must multiply by the derivative of the inside. We get:

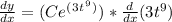

Now check if the derivative equals the right side of the original differential equation:

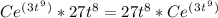
QED
I unfortunately do not have enough room for your second question. It is the exact same type of differential equation as the one solved above. The only difference is the fractional exponent, which would make the problem slightly more involved. If you ask your second question again on a different problem, I'd be glad to help you solve it.