Question

A motor is connected to the smaller 0.2 m radius pulley and cable, lifting 150 kg mass. Neglecting the mass/weight of the cable and pulley(s), find the torque necessary to accelerate the mass from 0 ms to 10 ms in 10 s (assume linear). Q4. 198.1 [Nm](a) 236.2 [Nm](b) 324.3 [Nm](c) 491.1 [Nm]

Answer 1

324.3Nm

Step-by-step explanation:

The torque is given by the equation

`\tau=r\ X\ F`

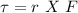
in this case the vectors r and F are perpendicular between them, thus:

`\tau=rF`

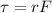
The forces acting on the mass are:

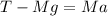`T-Mg=Ma` (1)

where T is the tension of the cable, M is the mass and a is the acceleration.

Furthermore, we have that the acceleration is:

`a=(v-v_0)/(t)=(10m/s-0m/s)/(10s)=1(m)/(s^2)`

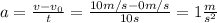
By replacing in (1) we can obtain:

`T=Ma-Mg=M(a-g)=(150kg)(1(m)/(s^2)+9.8\fac{m}{s^2})=1620N`

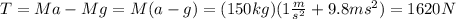
The force T produces the torque on the pulley, hence:

`\tau=rT=(0.2m)(1620N)=324Nm`

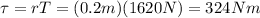
the answer is 324.4Nm

hope this helps!