Question

Lorena's mass is 27 kg. She climbs the 4.8 m ladder of a slide and reaches a velocity of 2.9 m/s at the bottom of the slide. How much work was done by friction on Lorena? Assume that air resistance is negligible.

Answer 1

1156.55 J

Step-by-step explanation:

From work-kinetic energy principles,

work done by gravity on Lorena, - work done by friction = kinetic energy change

work done by gravity on Lorena, = mgh where m = Lorena's mass = 27 kg and h = height of ladder = 4.8 m

work done by friction = W

kinetic energy change = 1/2m(v₂² - v₁²) where v₁ = initial velocity of Lorena = 0 and v₂ = final velocity of Lorena = 2.9 m/s

mgh - W = 1/2m(v₂² - v₁²)

W = mgh - 1/2m(v₂² - v₁²)

Substituting the values for the variables, we have

W = 27 kg × 4.8 m × 9.8 m/s² - 1/2 × 27kg ((2.9 m/s)² - 0²)

= 1270.08 J - 113.54 J

= 1156.55 J

Answer 2

The friction does -1156.5J of work on Lorena.

Step-by-step explanation:

From the law of conservation of mechanical energy, we know that the energy that Lorena has at the top of the slide must be equal to her energy at the bottom of the slide plus the work done by the friction. Since she only has gravitational potential energy at the top, and only kinetic energy at the bottom, we can express this as:

`U_0=K_f+W_f`

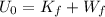
Where
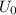`U_0` is the initial potential energy,
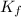`K_f` is the final kinetic energy and
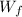`W_f` is the work done by the friction.

Now, since we know the expressions for gravitational potential energy and kinetic energy:

`U=mgh\\\\K=(1)/(2)mv^(2)`

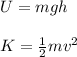
Where m is the mass of the body, g is the acceleration due to gravity, h is the height in which the body is, and v is the speed of the body.

We can substitute that expressions in our equation above like this:

`mgh_0=(1)/(2)mv_f^(2)+W_f`

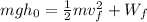
Solving for the work and computing, we obtain:

`W_f=mgh_0-(1)/(2)mv_f^(2)\\\\W_f=(27kg)(9.8m/s^(2))(4.8m)-(1)/(2)(27kg)(2.9m/s)^(2)\\ \\W_f=1156.5J`

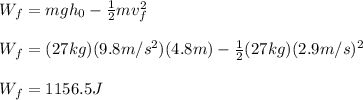
Since the friction is always opposite in direction to the motion, its work has always to be negative. So, the work done by the friction is -1156.5J.