Question

When air expands adiabatically (without gaining or losing heat), its pressure P and volume V are related by the equation PV1.4=C where C is a constant. Suppose that at a certain instant the volume is 320 cm3, and the pressure is 95 kPa (kPa = kiloPascals) and is decreasing at a rate of 11 kPa/minute. At what rate is the volume increasing at this instant?

Answer 1

26.47 cm³/minute

Step-by-step explanation:

We first differentiate the expression to obtain the rate of change of volume with time dV/dt

`PV^(1.4) = C\\ d(PV^(1.4))/dt = dC/dt\\1.4PV^(0.4)(dV)/(dt) + V^(1.4)(dP)/(dt) = 0\\1.4PV^(0.4)(dV)/(dt) = -V^(1.4)(dP)/(dt)\\ (dV)/(dt) = -(V)/(1.4P) (dP)/(dt)`

Now when V = 320 cm, P = 95 kPa and dP/dt = -11 kPa/minute since it is decreasing.

We substitute these values into the expression for dV/dt. So,

`(dV)/(dt) = -(V)/(1.4P) (dP)/(dt) = -(320 cm^(3) )/(1.4 X 95 kPa) X- 11 kPa/minute\\= 26.47 cm^(3)/minute`

Answer 2

26.466cm³/min

Step-by-step explanation:

Given:

Volume 'V'= 320cm³

P= 95kPa

dP/dt = -11 kPa/minute

pressure P and volume V are related by the equation

P
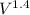`V^(1.4)`=C

we need to find dV/dt, so we will differentiate the above equation

`V^(1.4) (dP)/(dt) + P(d[V^(1.4) ])/(dt) = (d[C])/(dt)`

`(dP)/(dt) V^(1.4) + P(1.4)V^(0.4) (dV)/(dt) =0`

lets solve for dV/dt, we will have

`(dV)/(dt) =(-(dP)/(dt) V^(1.4) )/(P(1.4)V^(0.4) ) \\(dV)/(dt) =- (-(dP)/(dt) V)/(P(1.4))`

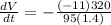`(dV)/(dt) = -((-11 ) 320)/(95(1.4))` (plugged in all the values at the instant)

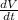`(dV)/(dt)` = 26.466

Therefore, the volume increasing at the rate of 26.466cm³/min at this instant