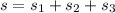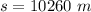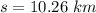Consider an old-fashion bicycle with a small wheel of radius 0.17 m and a large wheel of radius 0.92 m. Suppose the rider starts at rest, accelerates with a constant acceleration for 2.7 minutes to a velocity - QAmmunity.org

Consider an old-fashion bicycle with a small wheel of radius 0.17 m and a large wheel of radius 0.92 m. Suppose the rider starts at rest, accelerates with a constant acceleration for 2.7 minutes to a velocity

asked Sep 2, 2021 49.9k views

2 Answers

Answer:

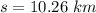
$s=10.26\ km$

Step-by-step explanation:

Given

initial velocity of bicycle,
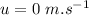
$u=0\ m.s^(-1)$

velocity of the bicycle after the first phase of acceleration,
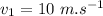
$v_1=10\ m.s^(-1)$

duration of first phase of uniform acceleration,
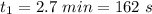
$t_1=2.7\ min=162\ s$

duration of second phase of zero acceleration,
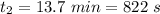
$t_2=13.7\ min=822\ s$

uniform velocity during the second phase,
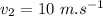
$v_2=10\ m.s^(-1)$

duration third phase of uniform deceleration,
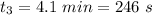
$t_3=4.1\ min=246\ s$

final velocity after the third phase of motion,
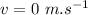
$v=0\ m.s^(-1)$

Now we find the acceleration in the first phase of motion:

a_1=(v_1-u)/(t_1)

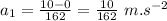
$a_1=(10-0)/(162) =(10)/(162)\ m.s^(-2)$

Now using the equation of motion:

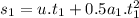
s_1=u.t_1+0.5a_1.t_1^2

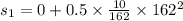
s_1=0+0.5* (10)/(162) * 162^2

$s_1=810\ m$ is the distance covered in the first phase of motion.

Distance covered in the third phase of motion:

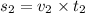
s_2=v_2* t_2

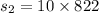
s_2=10* 822

$s_2=8220\ m$

Now we find the deceleration in the third phase of motion:

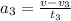
a_3=(v-v_3)/(t_3)

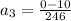
a_3=(0-10)/(246)

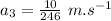
$a_3=(10)/(246)\ m.s^(-1)$

Now using the equation of motion:

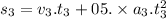
s_3=v_3.t_3+05.* a_3.t_3^2

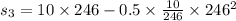
s_3=10* 246-0.5* (10)/(246) * 246^2

$s_3=1230\ m$ is the distance covered in the third phase of motion.

Hence the total distance covered by the bicycle in the whole incident is:

s=s_1+s_2+s_3

s=810+8220+1230

$s=10260\ m$

$s=10.26\ km$

Gilseung Ahn answered Sep 3, 2021

by Gilseung Ahn

6.1k points

Search QAmmunity.org