Question

A potter's wheel having a radius 0.50 m and a moment of inertia of 10.1 kg · m2 is rotating freely at 51 rev/min. The potter can stop the wheel in 4.0 s by pressing a wet rag against the rim and exerting a radially inward force of 74 N. Find the effective coefficient of kinetic friction between the wheel and the wet rag.

Answer 1

The effective coefficient of kinetic friction is 0.0682

Step-by-step explanation:

The kinetic energy is equal to the frictional work:

Ek = W

`E_(k) =(1)/(2) Iw^(2)`

Where

I = moment of inertia = 10.1 kg m²

w = angular velocity = 51 rev/min = 5.341 rad/s

`E_(k) =(1)/(2) 10.1*(5.341)^(2)` (eq. 1)

The frictional work is:

`W=\mu NX` (eq. 2)

The rotational expression of motion:

`X=(1)/(2) Rwt` (eq. 3)

Where

R = radially inward force = 74 N

t = 4

Using eq. 1, 2 and 3:

`(1)/(2)*10.1*(5.341)^(2) =\mu *74*0.5*(1)/(2) *(5.341)^(2) *4\\\mu =0.0682`

Answer 2

The effective coefficient of kinetic friction =0.3644

Step-by-step explanation:

Given Data:

r=0.50 m

I=moment of inertia = 10.1 kg · m^2

ω=51 rev/min=0.885 rev/sec

t=4.0 sec

F=74 N

Required:

the effective coefficient of kinetic friction between the wheel and the wet rag=?

Solution:

Angular Acceleration=α=2π*ω/t

Angular Acceleration=α=2π*0.85/4

Angular Acceleration=α=1.3351 rad/s^2

Torque=τ=μ*F*r=I*α

Where:

μ is co-officient of friction

μ
`=(I* \alpha)/(F*r)`

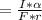
μ=
`(10.1*1.3351)/(74*0.50)=0.3644`

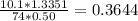
The effective coefficient of kinetic friction =0.3644