Question

The number of bacteria in a certain population increases according to a continuous exponential growth model, with a growth rate parameter of 5.3% per hour. How many hours does it take for the size of the sample to double?

Answer 1

The size of sample to double after 13.08 hours.

Explanation:

Formula of exponential growth

`A=A_0e^(rt)`

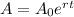
A=The number of bacteria after t time.

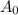`A_0` = The number of bacteria when t=0.

r= rate of growth

t= time.

The size of the sample will be double.

It means ,

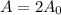`A=2 A_0`, r= 5.3%=0.053

`A=A_0e^(rt)`

`\Rightarrow 2 A_0=A_0e^(0.053t)`

`\Rightarrow 2 =e^(0.053t)`

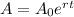
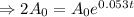
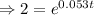
Taking ln both sides

`\Rightarrow ln(2) =ln(e^(0.053t))`

`\Rightarrow ln (2)= 0.053t`

`\Rightarrow t=( ln (2))/( 0.053)`

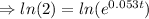
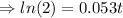
⇒t=13.08 h

The size of sample to double after 13.08 hours.