Question

An electron is trapped in an infinite square-well potential of width 0.2 nm. If the electron is initially in the n = 4 state, what are the various photon energies that can be emitted as the electron jumps to the ground state? (List in descending order of energy. Enter 0 in any remaining unused boxes.)

Answer 1

Please read the answer below

Step-by-step explanation:

The energies in a infinite square-well potential of width a is given by

`E=n^2(\pi^2\hbar^2)/(8m_ea)`

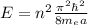
where me=9.1*10^{-31}kg, hbar=1.05*10^{-34}Js and a= 0.2*10^{-9}m.

From the state n=4 the electron can pass to state n=3, n=2 and n=1. The different transitions can be

n4->n3=E4-E3

n3->n2=E3-E2

n2->n1=E2-E1

Hence, by replacing we have that the photon energies emitted are given by

`T_(4-3)=E_4-E_3=(\pi^2\hbar^2)/(8m_ea)(4^2-3^2)=5.26*10^(-28)J\\T_(3-2)=E_3-E_2=(\pi^2\hbar^2)/(8m_ea)(3^2-2^2)=3.76*10^(-28)J\\T_(2-1)=E_2-E_1=(\pi^2\hbar^2)/(8m_ea)(2^2-1^2)=2.25*10^(-28)J`

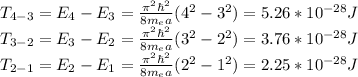
However, the transitions T4-2, T4-3, T3-1 are also allowed

`T_(4-2)=E_4-E_2=(\pi^2\hbar^2)/(8m_ea)(4^2-2^2)=9.04*10^(-28)J\\T_(4-1)=E_4-E_1=(\pi^2\hbar^2)/(8m_ea)(4^2-1^2)=1.12*10^(-27)J\\T_(3-1)=E_3-E_1=(\pi^2\hbar^2)/(8m_ea)(3^2-1^2)=6.01*10^(-28)J`

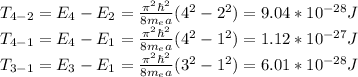
hope this helps!!