Answer:
a.
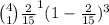 +
+
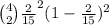 +
+
 +
+
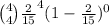
b.
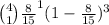 +
+
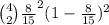
c.
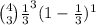
d.
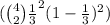 ×
×
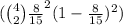
e.
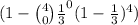 ×
×

Explanation:
Number of cars in lot = 30
Number of cars in great shape = 10
Number of cars in good shape = 16
Number of cars in poor shape = 4
The probability that a car selected is in great shape = 10/30
The probability that a car selected is in good shape = 16/30
The probability that a car selected is in poor shape = 4/30
Therefore, we have
When 4 cars are selected
P(Car is in poor shape) =
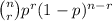
Where:
p = Probability of success = 2/15
n = Total number of count = 30
r = Number selected = 4
P =
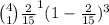 +
+
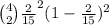 +
+
 +
+
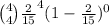
b. Here we have
P(At least two cars are in good shape) =
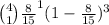 +
+
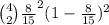
c. P(Exactly 3 cars are in great shape) =
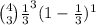
d. P(2 Great and 2 Good) =
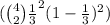 ×
×
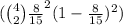
e. P(1 Great and 3 poor) =
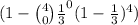 ×
×
