Question

Two long parallel wires are separated by 18 cm. One of the wires carries a current of 8 A and the other carries a current of 26 A. The permeabilty of free space is 1.257 × 10−6 N · m/A. Determine the magnitude of the magnetic force on a 2.1 m length of the wire carrying the greater current.

Answer 1

The magnitude of the magnetic force on the wire carrying greater current is is 4.85 x 10⁻⁴ N

Step-by-step explanation:

Given;

distance of separation of the two wires, d = 18 cm

current in the first wire, I₁ = 8 A

current in the second wire, I₂ = 26 A

length of the wire, L = 2.1 m

permittivity of free space, μ₀ = 4π x 10⁻⁷ N·m/A = 1.257 × 10⁻⁶ N·m/A

The magnitude of the magnetic force on the wire carrying greater current is given as;

`F_2 = (\mu_o I_1I_2L_2)/(2\pi d ) \\\\F_2 = (4\pi *10^(-7) *8*26*2.1)/(2\pi *0.18 )\\\\F_2 = 4.85 *10^(-4) \ N`

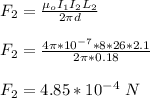
Therefore, the magnitude of the magnetic force on the wire carrying greater current is is 4.85 x 10⁻⁴ N

Answer 2

F=4.85*10^{-4}N

Step-by-step explanation:

The magnetic force due to the wire with lower current over the wire with greater current is given by:

`F=ilBsin\theta` (1)

where i is the current of the wire with greater current, l is the length and B is the magnetic field generated by the other wire. Hence, we have to compute the magnetic field by using the formula:

`B=(\mu_0I)/(2\pi r)`

where I is the current of the wire with lower current (8A), r is the distance between the wires (18cm=18*10^-2m) and mu0 is the space permeability. By replacing we have

`B=((1.257*10^(-6)Tm/A)(8A))/(2\pi (18*10^(-2)m))=8.89*10^(-6)T`

B and l are perpendicular to each other. Hence, by replacing in (1) we obtain:

`F=(26A)(2.1m)(8.89*10^(-6)T)=4.85*10^(-4)N`

F=4.85*10^{-4}N

hope this helps!!