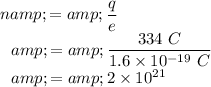Answer:
The number of electrons surplussed on each surface is
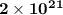 .
.
Step-by-step explanation:
Given:
The masses of the sphere,

The length of the strings,
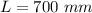
The angle made by each string with vertical,
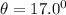
According to the diagram, the equilibrium condition for the vertical components of the forces acting on each sphere can be written as

The equilibrium condition for the horizontal components of the forces acting on each sphere can be written as

Here,
 is the electrostatic force experienced by the metal spheres.
is the electrostatic force experienced by the metal spheres.
The value of the electrostatic force is given by

Here,
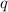 is the charge on each sphere and
is the charge on each sphere and
 is the distance between them.
is the distance between them.
Referring to the figure, from
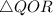 ,
,
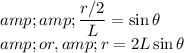
Substituting the value of
 in equation (3), we have
in equation (3), we have
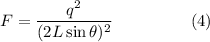
From equation (1),
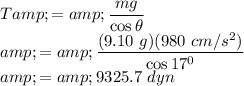
Substituting the values of
 and
and
 in equation (2), we have
in equation (2), we have
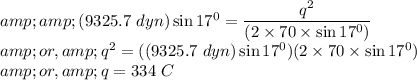
If
 is the number if electron surplussed with the metal sphere, then
is the number if electron surplussed with the metal sphere, then

Here,
 is the electronic charge.
is the electronic charge.
Substituting the value of
 and
and
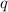 in equation (5), we have
in equation (5), we have