Answer:
Max possible red points = 220
Explanation:
- Remark that a convex quadrilateral has exactly one intersection which is the intersection of its two diagonals.
- Consider 9 points on the circle, which give at most ( combination ):
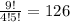 intersections.
intersections.
- Now consider the center and the three points on the circle, there are at most ( combinations ):
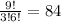 intersections.
intersections.
- So the total number of red points would be:
Given = 10
2 Diagonals = 126
Center + 3 pts = 84
======================
Max possible red points = 220
======================