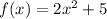Question

Find the particular solution of the differential equation that satisfies the initial condition f'(x) 4x, f(0) = 5 f(x) =

Answer 1

Answer:
`f(x)=2x^2+5`

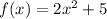
Explanation:

First integrate f'(x) so we can find the funtion f(x):

`4\int\limits {x} \, dx =4[(1)/(2) x^2]=2x^2+C=f(x)`

The initial conditions say that when x = 0, the function equals 5. Let's write that down:

`f(0)=5=2(0^2)+C=C`

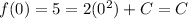
Therefore, the integration constant 'C' must equal 5. This means that our function is:

`f(x)=2x^2+5`